Regresión lineal en R, explorando un conjunto de datos del mundo real

#linear-regression

#oceanography

Publicado el 24 abr 2023

11 min de lectura

En este artículo exploraremos los conceptos fundamentales de la regresión lineal utilizando un conjunto de datos del mundo real. Utilizaremos la Base de datos de botellas que contiene una colección de datos oceanográficos, incluyendo temperatura, salinidad, densidad potencial y otros.

Este artículo no tiene como objetivo ser una introducción exhaustiva a la regresión lineal, sino más bien una guía práctica para que comiences a utilizar esta técnica en problemas del mundo real. Es importante tener en cuenta que aunque pueden existir técnicas más avanzadas para ciertas relaciones entre variables del conjunto de datos, nos enfocaremos en seleccionar a mano las variables más adecuadas para la regresión lineal.

Revisión Modelo de regresiónEnlace a este encabezado

En su forma más general, un modelo de regresión asume que la respuesta $Y$ puede ser expresada como una función de las variables predictoras $X_1, X_2, \cdots, X_n$ más un término de error $\epsilon$ :

Y = f(X_1, X_2, \cdots, X_n) + \epsilon

En esta forma, estimar $f$ puede ser bastante desafiante, incluso asumiendo que es una función suave y continua. Existen infinitas funciones posibles que se pueden utilizar, y los datos por sí solos no nos dirán cuál es la mejor. Aquí es donde entra en juego la linealidad. Al asumir que la relación entre las variables predictoras y la respuesta es lineal, podemos simplificar en gran medida el proceso de modelado. En lugar de estimar la función completa $f`, solo necesitamos estimar los parámetros desconocidos en la ecuación de regresión lineal:

Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_n X_n + \epsilon

Aquí, $\beta_0, \beta_1, \beta_2, \beta_n$ son parámetros desconocidos (también llamados término de intercepción o sesgo). Observa que las variables predictoras en sí no tienen que ser lineales. Por ejemplo, podemos tener un modelo de la forma:

Y = \beta_0 + \beta_1 log(X_1) + \beta_2 X_2^2 + \beta_3 X_3 X_1 + \epsilon

que aún es lineal. Mientras tanto:

Y = \beta_0 + \beta_1 \beta_2 X_1 + \beta_2 X_2 + \beta_3 X_3 + \epsilon

no lo es. Aunque el nombre implica una línea recta, los modelos de regresión lineal pueden ser bastante flexibles y pueden manejar conjuntos de datos complejos. Para capturar relaciones no lineales entre las variables predictoras y la respuesta, se pueden incluir términos cuadráticos en el modelo. Además, los predictores no lineales se pueden transformar a una forma lineal mediante transformaciones adecuadas, como la transformación logarítmica, que puede linearizar relaciones exponenciales.

En la práctica, casi todas las relaciones pueden ser representadas o reducidas a una forma lineal. Por eso la regresión lineal es tan ampliamente utilizada y popular. Es una técnica simple pero poderosa.

Representación matricialEnlace a este encabezado

Para facilitar el trabajo, presentemos nuestro modelo de una respuesta $Y$ y $n$ variables predictoras $X_1, X_2, \cdots, X_n$ en forma de tabla:

y_1 \quad x_{11} \quad x_{12} \quad \cdots \quad x_{1n} \\ y_2 \quad x_{21} \quad x_{22} \quad \cdots \quad x_{2n} \\ \vdots \\ y_m \quad x_{m1} \quad x_{m2} \quad \cdots \quad x_{mn}

donde $m$ es el número de observaciones o casos en el conjunto de datos. Dados los valores reales de los datos, podemos escribir el modelo como:

y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_n x_{in} + \epsilon_i

Podemos escribir esto de forma más conveniente en forma de matriz:

y = X \beta + \epsilon

donde $y = (y_1, y_2, \cdots, y_m)^T$ es el vector de respuesta, $\epsilon = (\epsilon_1, \epsilon_2, \cdots, \epsilon_m)^T$ es el vector de error, $\beta = (\beta_0, \beta_1, \cdots, \beta_n)^T$ es el vector de parámetros, y:

X = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1n} \\ 1 & x_{21} & x_{22} & \cdots & x_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{m1} & x_{m2} & \cdots & x_{mn} \end{bmatrix}

es la matriz de diseño. Observa que la primera columna de $X$ es toda de unos. Esto se hace para tener en cuenta el término de intercepción $\beta_0`.

Estimando los parámetrosEnlace a este encabezado

Con el fin de lograr el mejor ajuste posible entre nuestro modelo y los datos, nuestro objetivo es estimar los parámetros denotados como $\beta$ . Geométricamente, esto implica encontrar el vector $\beta$ que minimice la diferencia entre el producto $X\beta$ y la variable objetivo $y$ . Nos referimos a esta elección óptima de $\beta$ como $\hat{\beta}$ , que también se conoce como los coeficientes de regresión.

Para predecir la variable de respuesta, nuestro modelo utiliza la ecuación $\hat{y} = X \hat{\beta}$ o, equivalente, $Hy$ , donde $H$ representa una matriz de proyección ortogonal. Los valores predichos $\hat{y}$ se conocen comúnmente como los valores ajustados. Por otro lado, la discrepancia entre la respuesta real $y$ y la respuesta ajustada $\hat{y}$ se denomina residuo.

Estimación por mínimos cuadrados.Enlace a este encabezado

La estimación de $\beta$ puede abordarse tanto desde una perspectiva geométrica como no geométrica. Definimos la mejor estimación de $\beta$ como aquella que minimiza la suma de los residuos al cuadrado:

\sum{\epsilon_i^2} = \epsilon^T \epsilon = (y - X \beta)^T (y - X \beta)

Para encontrar esta estimación óptima, diferenciamos la expresión con respecto a $\beta$ y establecemos el resultado en cero, obteniendo las ecuaciones normales:

X^T X \hat{\beta} = X^T y

Curiosamente, también podemos derivar el mismo resultado utilizando un enfoque geométrico:

\begin{align} \hat{\beta} &= (X^T X)^{-1} X^T y \\ X \hat{\beta} &= X (X^T X)^{-1} X^T y \\ \hat{y} &= H y \end{align}

En este contexto, $H = X (X^T X)^{-1} X^T$ representa la matriz sombrero (hat matrix), que sirve como matriz de proyección ortogonal sobre el espacio de columnas generado por $X$ . Aunque $H$ es útil para manipulaciones teóricas, generalmente no se calcula explícitamente debido a su tamaño (una matriz de $n \times n$ ). En su lugar, se utiliza la pseudoinversa de Moore-Penrose de $X$ para calcular eficientemente $\hat{\beta}$ .

Es importante destacar que no calcularemos explícitamente la matriz inversa aquí, sino que utilizaremos la función lm incorporada en R para ello.

Acerca del conjunto de datosEnlace a este encabezado

El conjunto de datos de CalCOFI es un recurso extenso y completo, reconocido por su larga serie temporal que abarca desde 1949 hasta la actualidad. Con más de 50,000 estaciones de muestreo, es el repositorio más completo de datos oceanográficos y de peces larvales a nivel mundial.

Nuestro interés es determinar si existen variables que presenten una relación lineal con la temperatura del agua. Así que comencemos cargando los datos y obteniendo un resumen de las filas y columnas.

data <- read.csv("bottle.csv")
head(data, 10)

Puedes obtener más información sobre el significado de cada columna [aquí]((https://new.data.calcofi.com/index.php/database/calcofi-database/bottle-field-descriptions)

Limpiando los datosEnlace a este encabezado

Para mantener esta publicación del blog concisa y fácil de leer, nos centraremos en cinco variables clave: temperatura, salinidad, oxígeno disuelto por litro, profundidad en metros y densidad potencial. Estas variables serán nuestros puntos de interés principales. Sin embargo, no dudes en explorar cualquier otra variable que llame tu atención.

Para mantener la integridad de los datos, vale la pena mencionar que existen algunos valores faltantes dentro del conjunto de datos. Pero podemos manejar esto fácilmente utilizando la función na.omit(). Esta función nos permite eliminar las filas con valores faltantes, asegurando un análisis sólido.

data <- data[, c("T_degC", "Salnty", "O2ml_L", "Depthm, T_degC")]
data <- na.omit(data)

Revisando linealidadEnlace a este encabezado

Queremos asegurarnos de que se cumplan las suposiciones del modelo lineal. Esto se puede comprobar calculando los coeficientes de correlación. Un coeficiente de correlación cercano a cero indica que no hay una relación lineal entre las dos variables, mientras que un coeficiente de correlación cercano a -1 o 1 indica que hay una fuerte relación lineal negativa o positiva. Podemos crear una matriz de correlación utilizando la función cor().

library(corrplot)

correlation_matrix <- cor(data)
corrplot(correlation_matrix, method = "circle")

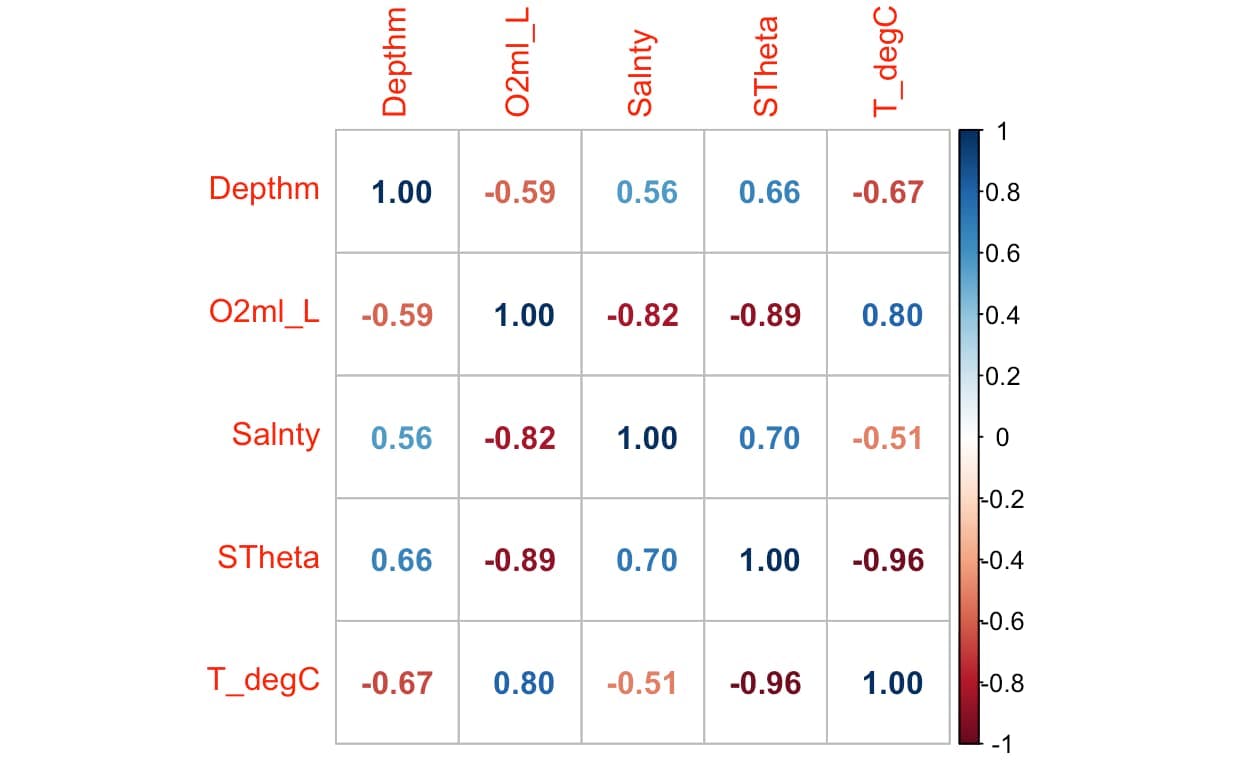
Matriz de correlación

Centremos nuestra atención en las variables que muestran una correlación más fuerte: T_degC y STheta. Dado que tenemos la flexibilidad para dar forma a nuestra exploración en este escenario, podemos decidir en qué aspectos profundizar y cómo abordarlos. Sin embargo, en un escenario del mundo real, las variables a analizar suelen estar dictadas por el problema específico en cuestión.

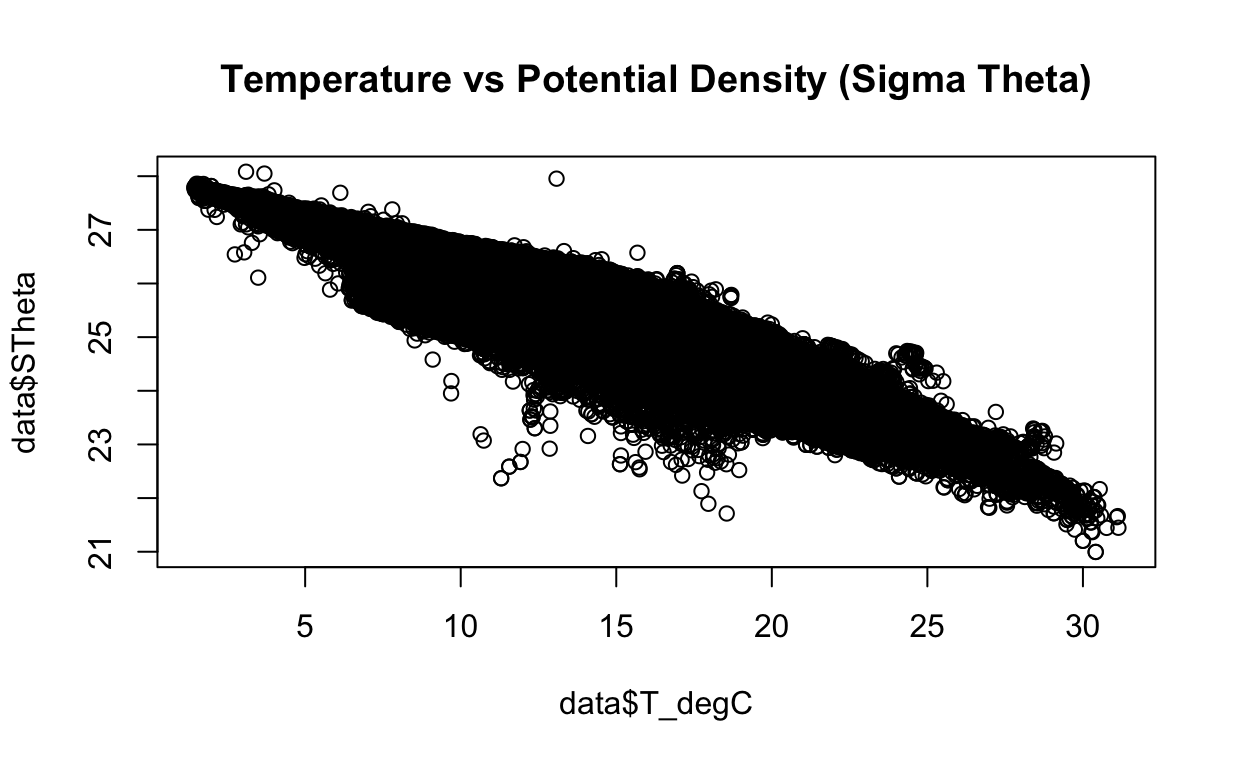
Para comenzar nuestro análisis, grafiquemos estas variables y examinemos si existe una relación lineal entre ellas. Esta visualización inicial nos proporcionará información valiosa sobre su posible conexión.

plot(data$T_degC, data$STheta,
 main = "Temperature vs Potential Density (Sigma Theta)")

variable plot

Buscando valores atípicosEnlace a este encabezado

Los valores atípicos son puntos de datos que están lejos de los demás puntos de datos. Pueden ser causados por errores experimentales, corrupción de datos u otras anomalías. Los valores atípicos pueden tener un gran efecto en el modelo de regresión lineal, ya que pueden influir desproporcionadamente en el ajuste del modelo. Podemos utilizar la función boxplot() para visualizar los valores atípicos.

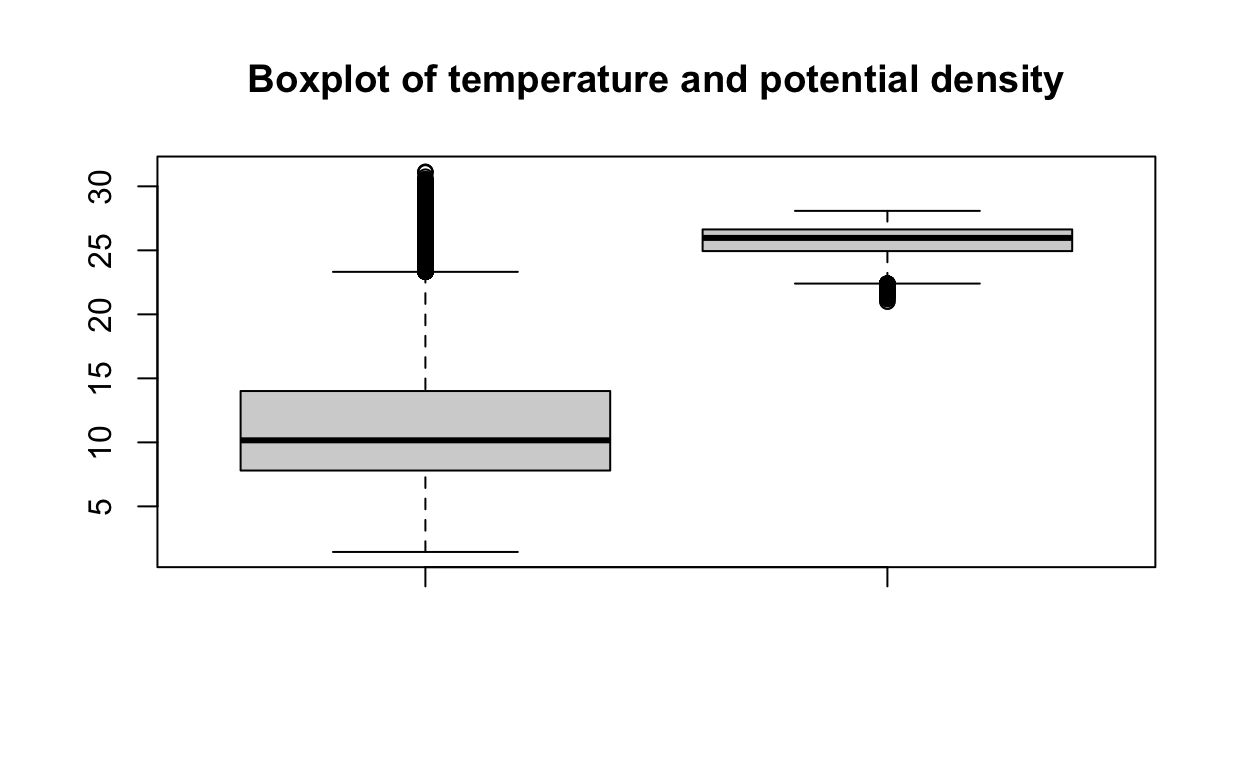
boxplot(data$T_degC, data$O2ml_L,
 main = "Boxplot of temperature and dissolved oxigen per litter")

Al observar el gráfico, parece que puede haber algunos puntos de datos que podrían considerarse valores atípicos. Sin embargo, en este análisis, optaremos por mantener estos puntos. Parecen estar dentro de un rango razonable y no están significativamente alejados de la mediana. Si estás interesado en explorar técnicas más precisas para la detección de valores atípicos, puedes consultar este útil recurso aquí

variable plot

Creando el modeloEnlace a este encabezado

Para asegurar una evaluación efectiva del rendimiento de nuestro modelo, dividiremos los datos en conjuntos de entrenamiento y prueba. Esta división nos permite entrenar nuestro modelo en un subconjunto de los datos y evaluar su precisión en datos no vistos.

Con este propósito, asignaremos el 80% de los datos al entrenamiento y reservaremos el 20% restante para la prueba. Para lograr esto, podemos utilizar la función sample(), que nos permite seleccionar aleatoriamente las filas que constituirán el conjunto de entrenamiento. Esta selección aleatoria garantiza una muestra representativa y evita sesgos en el entrenamiento del modelo.

training_rows <- sample(1:nrow(data), 0.8 * nrow(data))
training_data <- data[training_rows, ]
testing_data <- data[-training_rows, ]

Ahora podemos crear el modelo lineal utilizando la función lm(). El primer argumento es la fórmula, que es la variable de respuesta (energía de densidad potencial) seguida de la variable predictora (temperatura). El segundo argumento es el conjunto de datos que se utilizará para crear el modelo.

model <- lm(STheta ~ T_degC, data = training_data)

Podemos utilizar la función summary() para obtener un resumen del modelo.

summary(model)

Call:
lm(formula = STheta ~ T_degC, data = training_data)

Residuals:
    Min      1Q  Median      3Q     Max
-3.3407 -0.1381 -0.0088  0.1076  2.0716

Coefficients:
              Estimate Std. Error t value Pr(>|t|)
(Intercept)  2.831e+01  1.020e-03   27769   <2e-16 ***
T_degC      -2.305e-01  8.712e-05   -2645   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2676 on 529012 degrees of freedom
Multiple R-squared:  0.9297,	Adjusted R-squared:  0.9297
F-statistic: 6.997e+06 on 1 and 529012 DF,  p-value: < 2.2e-16

Primero, vamos a explicar la salida de la función summary():

La tabla Coefficients muestra los coeficientes estimados del modelo lineal.
La columna Estimate muestra la intersección y la pendiente del modelo lineal.
La columna Pr(>|t|) muestra el valor p de los coeficientes.
El valor p indica si el coeficiente es estadísticamente significativo.
El Residual standard error es la desviación estándar de los residuos.
El Multiple R-squared es la proporción de la varianza en la variable de respuesta que se explica por los predictores.
El Adjusted R-squared es el R-cuadrado ajustado por el número de predictores en el modelo.
El F-statistic es la relación entre la suma promedio de cuadrados de regresión y la suma promedio de cuadrados de error.
El valor p del F-statistic indica si el modelo es estadísticamente significativo.

Según el valor p de los coeficientes, podemos concluir que la intersección y la pendiente son estadísticamente significativas.

Haciendo prediccionesEnlace a este encabezado

odemos utilizar la función predict() para hacer predicciones en el conjunto de pruebas. El primer argumento es el modelo y el segundo argumento es el conjunto de datos que se utilizará para hacer las predicciones. La función predict() devuelve un vector de predicciones.

predictions <- predict(model, testing_data)

Podemos utilizar la función plot() para graficar los valores reales vs los valores predichos.

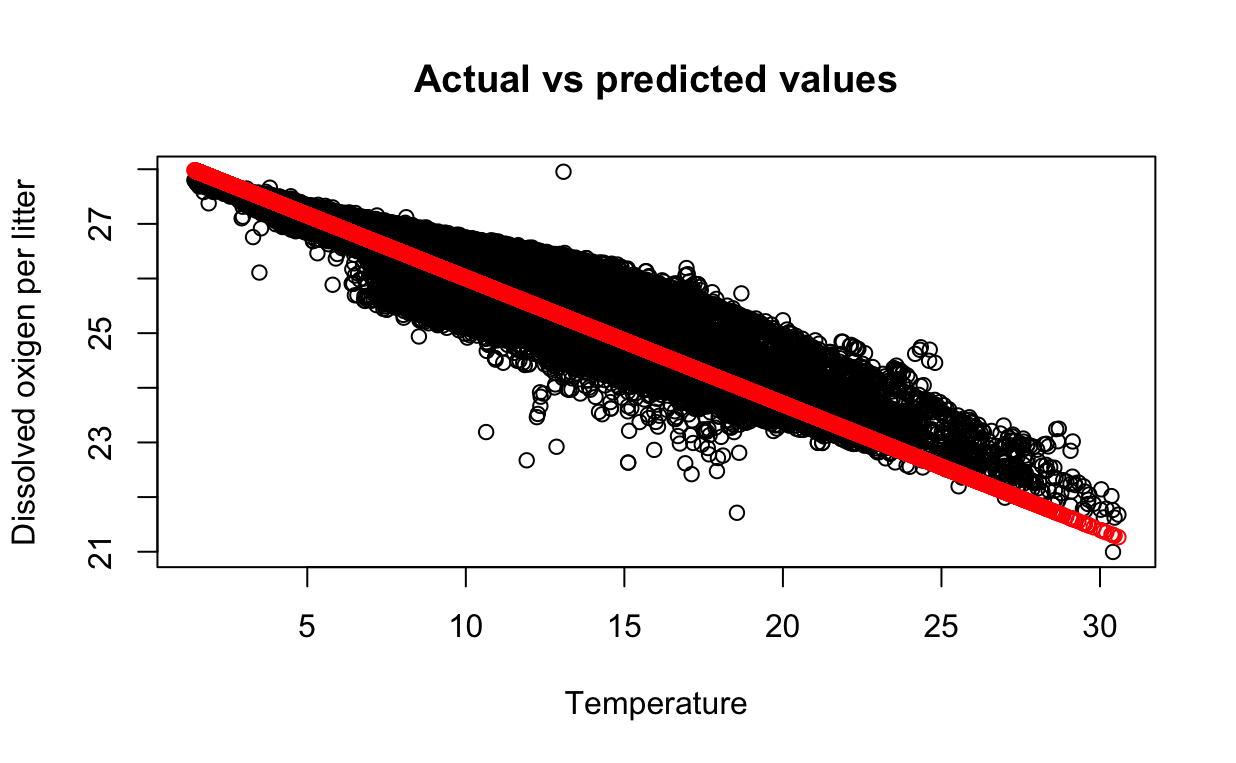
plot(testing_data$T_degC, testing_data$STheta,
  main = "Actual vs predicted values",
  xlab = "Temperature", ylab = "Potential density")

points(testing_data$T_degC, predictions, col = "red")

Los puntos rojos son los valores predichos y los puntos azules son los valores reales. Podemos ver que los valores predichos están cerca de los valores reales.

variable plot

ReferenciasEnlace a este encabezado

Faraway, Julian J. Linear Models with Python. CRC Press, 2021.
Heumann, Christian, and Micheal Schomaker Shalabh. Introduction to statistics and data analysis. Springer, 2016.